ENCCS - EMTO Tutorial No.2 - Calculate Elastic Constant of Cubic Lattice

EMTO Tutorial No.2 – Calculate Elastic Constant of Cubic Lattice

on March 15, 2024

EMTO-CPA is a state-of-the-art approach for investigating the electronic structure and properties of substitutional disordered system within the framework of density-functional theory (DFT). It employs the Exact Muffin-Tin Orbitals (EMTO) to represent the single-electron wave functions for the optimised overlapping muffin-tin (OOMT) potential. In this tutorial we will showcase how to calculate the elastic constant of a cubic lattice.

ENCCS currently provides support and contributes to the development under EMTO’s license through a proof of concept (POC) project.

This Tutorials series will be for new users of EMTO and only focus on “how”. If you are interested with the theory behind EMTO-CPA code please reading the Book by Professor Levente Vitos.

Links:

EMTO official webpage: emto.gitlab.io
Manual: https://emto.gitlab.io/manual/manual.html
Book by Prof. Levente Vitos: Computational Quantum Mechanics for Materials Engineers

Units:
• length: Bohr
• energy: Rydberg

Wigner–Seitz Radius

EMTO input file follows a very strict format, even one extra space may causes problems. Please use replace in the editor when you manually modify the input values.

Deformation Matrix for Cubic Lattice

More detailed information about this part, people could read the Chapter 6.2 from the book by Prof. Levente Vitos: Computational Quantum Mechanics for Materials Engineers.

Orthorhombic distortion

D_o(\delta_o) + I = \left[\begin{matrix} 1+\delta_o&0&0\\ 0&1-\delta_o&0\\ 0&0&\frac{1}{(1-\delta_o^2)}\\ \end{matrix}\right]

leads to energy change

\Delta E(\delta_o) = 2Vc'\delta_o^2+O(\delta_o^4)

Monoclinic distortion

D_m(\delta_m) + I = \left[\begin{matrix} 1&\delta_m&0\\ \delta_m&1&0\\ 0&0&\frac{1}{(1-\delta_m^2)}\\ \end{matrix}\right]

leads to energy change

\Delta E(\delta_m) = 2Vc_{44}\delta_m^2+O(\delta_m^4)

B=\frac{1}{3}(c_{11}+2c_{12})

c'=\frac{1}{2}(c_{11}-c_{12})

From EMTO tutorial No.1, we could get bulk modulus $B$ by calcuted the equation of state (EOS), from above relations people could get all 3 independent elastic constants $c_{11}$ , $c_{12}$ and $c_{44}$ .

there are many ways of doing the lattice distortion to get the elastic constants. Here for EMTO code we choose an isochoric stain, $det(D+I)=1$ , will keep the volume of the unit cell, so the radial mesh will be keep the same for different stain to reduce the numerical error.
The orthorhombic and monoclinic distortion will only keep the even order of $\delta$, we could only do the calculations for $\delta > 0, (0.01, 0.02 … 0.05)$

After the distortion $D_o$ apply to the FCC lattice, its symmetry will be changed to face center orthorhombic (fco), for BCC will be body center orthorhombic (bco).
After the distortion $D_m$ apply to the FCC lattice, its symmetry will be changed to body center orthorhombic (bco), for BCC will be face center orthorhombic (fco).

	FCC	BCC
$D_o$	fco	bco
$D_m$	bco	fco

Perform the calculations of Elastic Constants for FCC Copper

Input files for these calculations we could find from the examples shipped with EMTO source code. Here are the files and folders:

> tree
.
├── bmdl
│   ├── bco0.dat
│   ├── bco1.dat
│   ├── bco2.dat
│   ├── bco3.dat
│   ├── bco4.dat
│   ├── bco5.dat
│   ├── fco0.dat
│   ├── fco1.dat
│   ├── fco2.dat
│   ├── fco3.dat
│   ├── fco4.dat
│   ├── fco5.dat
│   └── mdl/
├── kfcd
│   ├── cuf0.dat
│   ├── cuf1.dat
│   ├── cuf2.dat
│   ├── cuf3.dat
│   ├── cuf4.dat
│   ├── cuf5.dat
│   ├── cuo0.dat
│   ├── cuo1.dat
│   ├── cuo2.dat
│   ├── cuo3.dat
│   ├── cuo4.dat
│   └── cuo5.dat
├── kgrn
│   ├── chd/
│   ├── cuf0.dat
│   ├── cuf1.dat
│   ├── cuf2.dat
│   ├── cuf3.dat
│   ├── cuf4.dat
│   ├── cuf5.dat
│   ├── cuo0.dat
│   ├── cuo1.dat
│   ├── cuo2.dat
│   ├── cuo3.dat
│   ├── cuo4.dat
│   ├── cuo5.dat
│   └── pot/
├── kstr
│   ├── bco0.dat
│   ├── bco1.dat
│   ├── bco2.dat
│   ├── bco3.dat
│   ├── bco4.dat
│   ├── bco5.dat
│   ├── fco0.dat
│   ├── fco1.dat
│   ├── fco2.dat
│   ├── fco3.dat
│   ├── fco4.dat
│   ├── fco5.dat
│   └── smx/
└── shape
    ├── bco0.dat
    ├── bco1.dat
    ├── bco2.dat
    ├── bco3.dat
    ├── bco4.dat
    ├── bco5.dat
    ├── fco0.dat
    ├── fco1.dat
    ├── fco2.dat
    ├── fco3.dat
    ├── fco4.dat
    ├── fco5.dat
    └── shp/

10 directories, 60 files

Bash

The cuf?.dat will be copper with fco distortions:

grep mdl kgrn/cuf?.dat

kgrn/cuf0.dat:FOR004=../bmdl/mdl/fco0.mdl
kgrn/cuf1.dat:FOR004=../bmdl/mdl/fco1.mdl
kgrn/cuf2.dat:FOR004=../bmdl/mdl/fco2.mdl
kgrn/cuf3.dat:FOR004=../bmdl/mdl/fco3.mdl
kgrn/cuf4.dat:FOR004=../bmdl/mdl/fco4.mdl
kgrn/cuf5.dat:FOR004=../bmdl/mdl/fco5.mdl

Bash

the cuo?.dat will be for bco distortions.

grep mdl kgrn/cuo?.dat

kgrn/cuo0.dat:FOR004=../bmdl/mdl/bco0.mdl
kgrn/cuo1.dat:FOR004=../bmdl/mdl/bco1.mdl
kgrn/cuo2.dat:FOR004=../bmdl/mdl/bco2.mdl
kgrn/cuo3.dat:FOR004=../bmdl/mdl/bco3.mdl
kgrn/cuo4.dat:FOR004=../bmdl/mdl/bco4.mdl
kgrn/cuo5.dat:FOR004=../bmdl/mdl/bco5.mdl

Bash

Now let’s recap a few things learned from the EMTO tutorial NO.1:

Keep in mind all these kstr, bmdl, shape results could be reused by any elastic constants calculation for FCC materials within a primitive unit cell with only one base site setup.

Setup the equilibrium SWS=2.6876 from the EOS calculation for all kgrn input files (also SOFC.= Y).
Maybe you should need to reduce the charge mixing by change with AMIX...= 0.020.
Because of the lower symmetry, non-equivalent k-points will be much larger compare to the FCC case. People could consider to use more cpu cores by export OMP_NUM_THREADS=4, e.g use 4 cpu cores, to accelerate the job.
Finish all these calculations follow the EMTO subprogram running dependency.
Make sure the convergence of all the kgrn calculations.
Get the total energies for different distortions from kfcd output.

in kfcd folder,

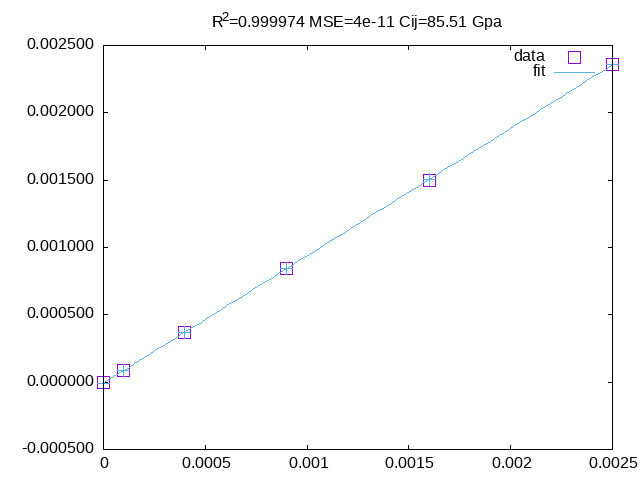
grep TOT-PBE cuo?.prn | awk '{if(NR==1)e0=$5;printf "%s %.6f %.6f\n" $1,NR*NR*0.0001,$5-e0}'

Bash

fit $\delta_o^2$ vs $\Delta E$ with the 2nd and 3th column to get $\c'$ .

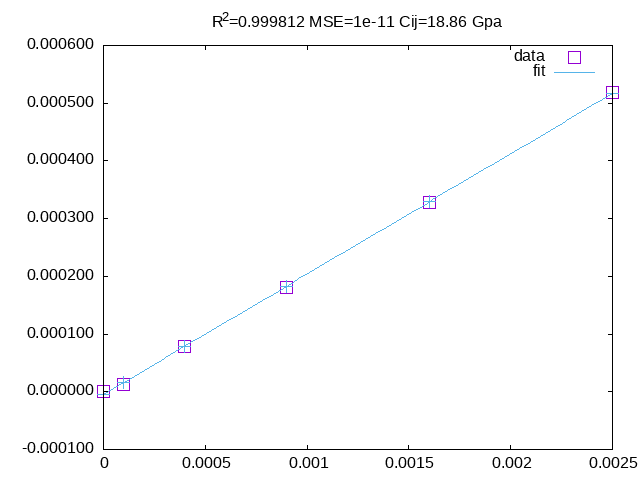
grep TOT-PBE cuf?.prn | awk '{if(NR==1)e0=$5;printf "%s %.6f %.6f\n" $1,NR*NR*0.0001,$5-e0}'

Bash

fit $\delta_m^2$ vs $\Delta E$ with the 2nd and 3th column to get $c_{44}$ .

Acknowledgments

EMTO-CPA code was created at KTH Royal Institute of Technology in Stockholm by Prof. Levente Vitos and his co-workers since 2000. It has been widely used to explore and design complex alloy systems, especially stainless steels and high entropy alloys (HEA) / Multi-Principal Element Alloys (MPEA).

Categories:

Tutorials

Tags:

emto